The statements which follow are concerned with the distribution of the total gas volumes of different real polyhedron foam glasses across the gas content of all of their polyhedron bubbles and across the volume of all spherical pores in their cell wall films as well as with the”mean section lengths” defined later determined stereologically1) for each cell.
If within the porosity n of a foam glass body of density ρ the ratio between the total volume of all pores and its external volume is known, then after carrying out a simple mass balance, the relationship
1)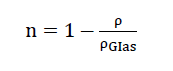
Here ρGlas means the density of the solid glass base material on which the foam glass body is based.
With the aid of x-ray investigations on samples which were sintered from waste glass powder with a temperature profile suitable for foam glass expansion, it was possible to determine that the base material of the foam glass can be assumed to be chemically identical to normal glass. It has a density of
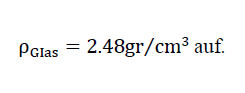
This condition was also confirmed using pycnometer measurements of the density of base material powder (0 ≤ ϕ ≤ 63μ)
processed from a cylinder mill of foam glass test pieces.
The observed values for the porosity n of the polyhedron foam glasses produced by us vary between 64 % and 90 % for the fine-celled polyhedron foam glass and between 82 % and 90 % for the foam glass types 1 and 2.
If the porosity n* means the ratio between the pore volume in all cell wall films of a polyhedron having a homogeneous structure
- 1)Stereology deals with the problem of how the three-dimensional structure of a body can be identified from a two-dimensional section.
foam glass body and its total volume as well as ρ* its density, then analogously to Formula No. 1 we have the relationship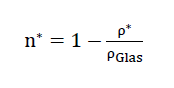
for the cell wall films on their own.
Based on this relationship it was obvious to directly determine the porosity n* by measuring the densities * of the cell wall films from spherical foam glass. Since the density ρ* of the spherical foam wall films to our knowledge can only be determined using a pycnometer, the test pieces - which had first been subjected to a static fracture test - were crushed, and those pieces whose dimensions were suitable for determining the density ρ* sieved out and boiled in chemically pure water1). Then after cooling to room temperature, the densities ρ* of the cell wall films determined according to the pycnometer measurement.
The diagram on fig. No. 6 shows points, whose coordinates give the values p and n*, which were measured on test pieces extracted from the sample series of the foam glass types 1 and 2. As the diagram identifies, for the sample of foam glass type 2, which were expanded at relatively low temperatures, a clear regression exists2)
3)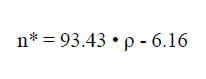
between the porosity n* (%) and the density ρ (g/cm3)
Conversely, for the foam glass type 1 samples, expanded at relatively high temperatures, such a relationship could no longer be identified.
- 1)The mixture of shards and water (chemically pure) had to be boiled to avoid gas accumulations on the cell wall shards, which would give false measurements of shard density ρ *.
- 2)The regression is however only certain within the defined range 0.26 ≤ ρ ≤ 0.35gr / cm3 .
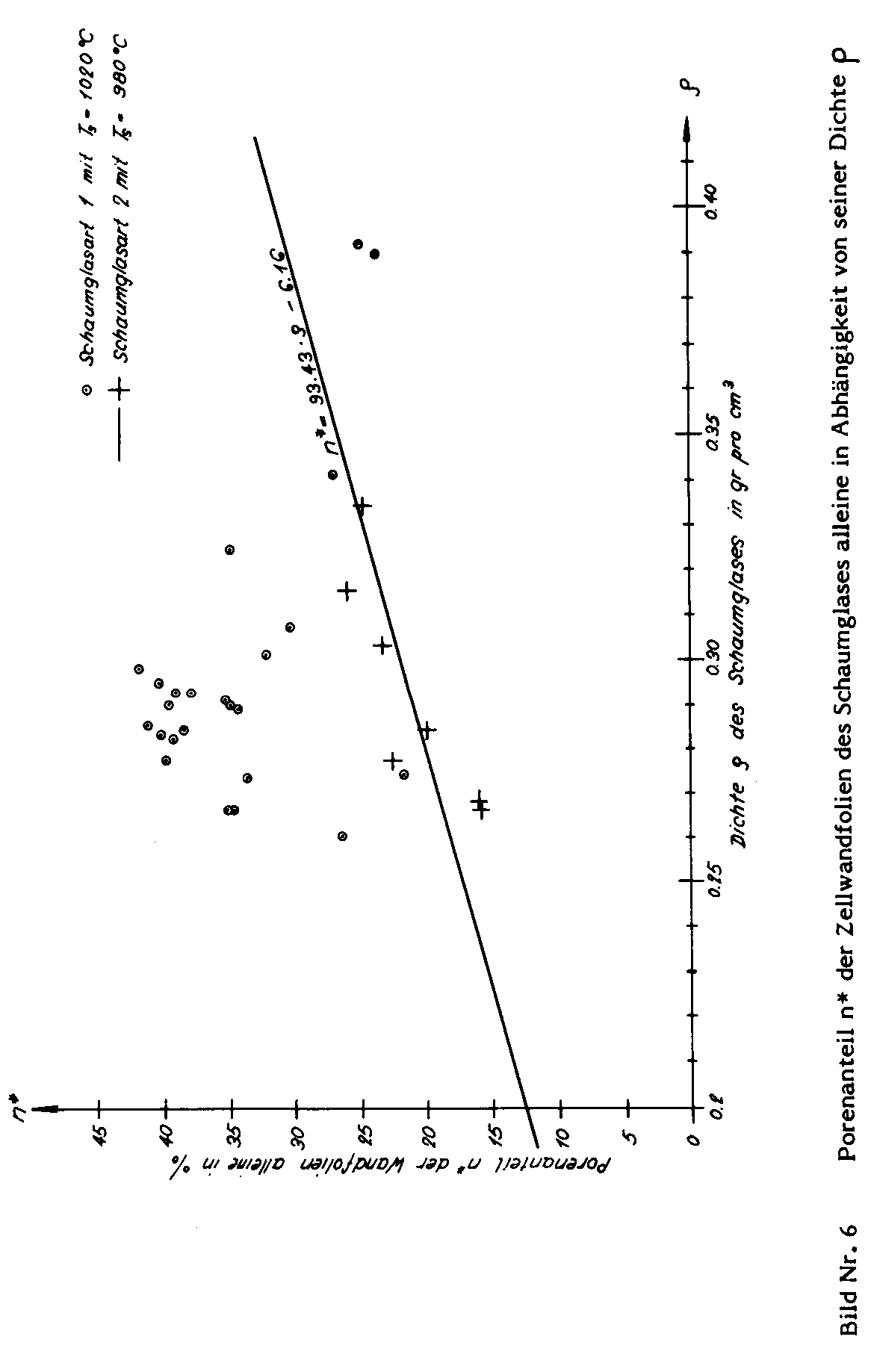
If we take nz be the ratio between the gas volume included in the polyhedron bubbles of a polyhedron foam glass sample and the sample volume as well as the symbol ω o mean the ratio 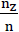 then after taking into account the parameters n and n* defined further above, as well as carrying out a simple volume balance, this leads to the algebraic relationship
then after taking into account the parameters n and n* defined further above, as well as carrying out a simple volume balance, this leads to the algebraic relationship
4)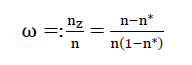
which will be used repeatedly later on.
.
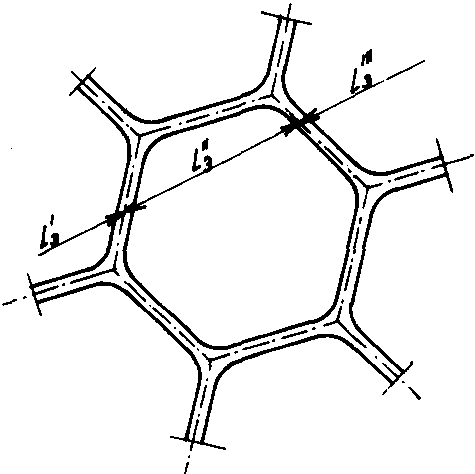
Fig. No. 7 Definition of the mean section length L̅3
If one imagines lines laid in all directions of a space filled with a given polyhedron foam glass type, then these are cut by the cell structure formed by the elementary polyhedra in innumerable unequally long sections 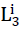 (see Fig. No. 7). The arithmetic mean of these partial sections is
(see Fig. No. 7). The arithmetic mean of these partial sections is
5)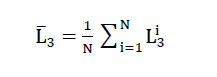
And is described as “mean section length” in stereology (5). This length L̅3, which can also be indicated as the “mean sectional length” of the space-pervading elementary polyhedron of the cell structure of the polyhedron foam glass on a test line, is roughly equivalent to the general term “cell size”. It was measured on the polyhedron foam glass samples investigated in this dissertation with the aid of the stereological equation
6)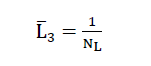
indirectly by determining the parameter NL. Here NLmeans the number of sections of the base polyhedron of the cell structure of the foam glass per unit length of the test line in a two-dimensional cutting plane (5).
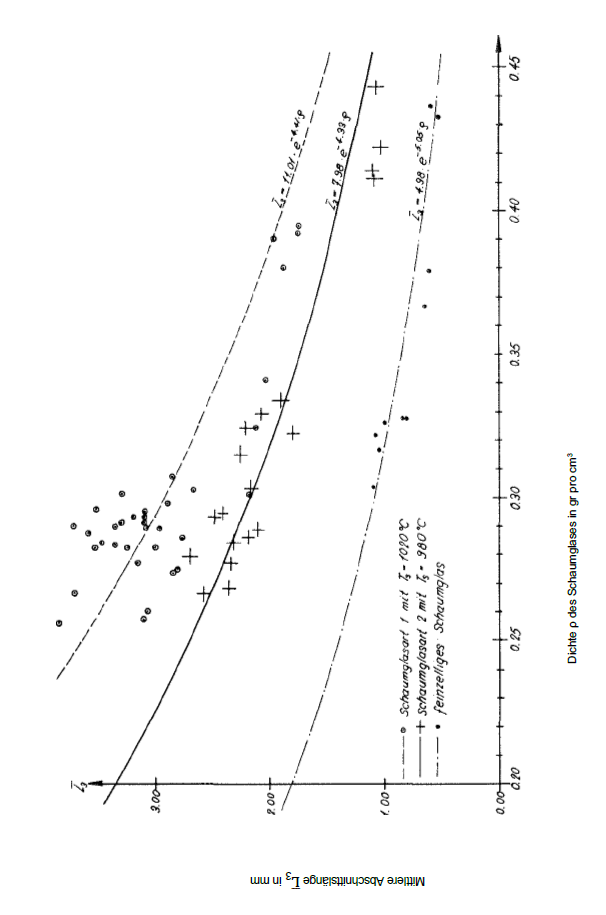
The coordinates (ρ,L3) of the points drawn in on the diagram on Fig. No. 8 was measured on samples of foam glass type 1 and 2 as well as the fine-celled polyhedron foam glass. In the same diagram the curves were added for the measurement points mentioned above for the non-linear regression equations
7)
for the foam glass type 1 and
8)
foam the glass type 2 as well ass
9)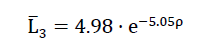
for the fine-celled polyhedron foam glass.
All three regressions for each of the foam glass types considered show a clear relationship between the density ρ[gr / cm3] and the “mean sectional length" L̅3 ( mm) of its base polyhedron. The diagram also shows how at constant density ρ the dimensions of their base polyhedra increase with increasing foam temperature Ts .
Bild Nr. 8 Die Mittlere Abschnittslänge L̅3 des Schaumglases in Abhängigkeit von seiner Dichte ρ